Задания по всем категориям
19. Найдите геометрия (1)
Найдите угол BEA, CE, AC 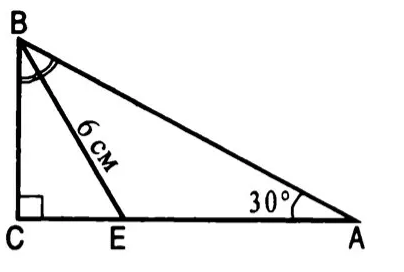

Изображение
Сложность:2
Макс.баллов:2
Ответ: _______________________
18. Решите уравнение (1)
Решите уравнение: $$4(2y-3)=3(y+5)-(y-1)$$
Сложность:2
Макс.баллов:2
Ответ: _______________________
17. Подставьте (2)
Подставьте $$x=-2$$ и найдите значение выражения $$\frac{3x^2-5x+4}{x-1}$$
Сложность:2
Макс.баллов:2
Ответ: _______________________
16. Упростите (1)
Упростите выражение:
$$5a−3(2a−4)+7$$
Сложность:2
Макс.баллов:2
Ответ: _______________________
15. Функциональный анализ
Определение нормы:
$$\|x\| \geq 0, \|x\| = 0 \Leftrightarrow x = 0$$
$$\|\alpha x\| = |\alpha| \cdot \|x\|$$
$$\|x + y\| \leq \|x\| + \|y\|$$
Норма в пространстве $$L_p:$$
$$\|f\|_p = \left( \int_{\Omega}|f(x)|^p dx \right)^{1/p}, \quad 1 \leq p < \infty$$
$$\|f\|_{\infty} = \operatorname{ess} \sup_{x \in \Omega} |f(x)|$$
Неравенство Гёльдера:
$$\|fg\|_1 \leq \|f\|_p \cdot \|g\|_q, \quad \frac{1}{p} + \frac{1}{q} = 1$$
Примеры
- Формула дискриминанта для решения квадратных уравнений
Ответы
- $x = (-b ± \sqrt(b² - 4ac)) / 2a$
- $\text{альтернатива}$
Сложность:3
Макс.баллов:20
| Ответ: | A |
|---|---|
14. Комбинаторика и теория вероятностей
Число размещений из n по k:
$$A_n^k = \frac{n!}{(n-k)!}$$
Число сочетаний из $n$ по $k$:
$$C_n^k = \binom{n}{k} = \frac{n!}{k!(n-k)!}$$
Формула полной вероятности:
$$P(A) = \sum_{i=1}^{n}P(B_i)P(A|B_i)$$
Формула Байеса:
$$P(B_i|A) = \frac{P(B_i)P(A|B_i)}{\sum_{j=1}^{n}P(B_j)P(A|B_j)}$$
Сложность:2
Макс.баллов:15
Ответ: _______________________
13. Статистические формулы
Формула среднего арифметического:
$$\bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_i$$
Формула выборочной дисперсии:
$$s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2$$
Формула стандартного отклонения:
$$s = \sqrt{s^2} = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2}$$
Формула доверительного интервала:
$$\bar{x} \pm t_{\alpha/2,n-1} \frac{s}{\sqrt{n}}$$

Без имениyy
| 
ugugih
|
ВОПРОСЫ
- Еще одна КРАСИВАЯ формула дискриминанта квадратного уравнения
ОТВЕТЫ
- \(x = (-b ± \sqrt{(b² - 4ac))} / 2a\)
Сложность:2
Макс.баллов:15
| Ответ: | A |
|---|---|
12. Физические формулы
Закон Гука для идеальной пружины:
$$F = -kx$$
Закон всемирного тяготения:
$$F = G \frac{m_1 m_2}{r^2}$$
Уравнение Шрёдингера (стационарное):
$$\hat{H}\Psi = E\Psi$$
Преобразования Лоренца:
$$\begin{cases}
x' = \gamma(x - vt) \\
t' = \gamma(t - \frac{vx}{c^2})
\end{cases}$$
где $$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$$
ВОПРОСЫ
- Основные формулы для законов Ньютона
ОТВЕТЫ
- F = ma, где F - сила, m - масса, a - ускорение'
- F₁ = -F₂ (третий закон Ньютона)
Сложность:3
Макс.баллов:20
| Ответ: | A |
|---|---|
11. Комбинированные формулы
$$\int_{0}^{\infty} e^{-x^2} dx = \frac{\sqrt{\pi}}{2}$$
$$\begin{cases} a, & \text{если } x > 0 \\ b, & \text{иначе} \end{cases}$$
При решении задачи учтите следующие свойства:
1. Интеграл от нечетной функции по симметричному отрезку равен нулю
2. Интеграл от четной функции по симметричному отрезку равен удвоенному интегралу по половине отрезка $$\int_{-a}^{a} f(x) dx = \begin{cases} 0, & \text{если } f(-x) = -f(x) \\ 2\int_{0}^{a} f(x) dx, & \text{если } f(-x) = f(x) \end{cases}$$
| Заголовок 2 | |
|---|---|

Без имениyy
| 
ugugih
|
ВопросЫ
- Формула дискриминанта для решения квадратных уравнений
Ответы
- $x = (-b ± \sqrt(b² - 4ac)) / 2a$
- $\text{альтернатива}$
Сложность:2
Макс.баллов:16
| Ответ: | A |
|---|---|
10. Нормализация баз данных
Привести заданную схему к третьей нормальной форме
Сложность:4
Макс.баллов:20
Ответ: _______________________
9. Основы SQL
Разработать схему базы данных и написать запросы для заданного сценария
ВОПРОСЫ
- Основные SQL запросы и их синтаксис
ОТВЕТЫ
- SELECT * FROM table WHERE condition
- CREATE TABLE, INSERT INTO, UPDATE, DELETE
Сложность:3
Макс.баллов:20
| Ответ: | A |
|---|---|
8. Кинематика
Решить задачи на расчет траектории, скорости и ускорения
Сложность:2
Макс.баллов:10
Ответ: _______________________
7. Законы Ньютон
Решить задачи на применение законов Ньютона
ВОПРОСЫ
- Основные формулы для законов Ньютона
ОТВЕТЫ
- F = ma, где F - сила, m - масса, a - ускорение'
- F₁ = -F₂ (третий закон Ньютона)
Сложность:2
Макс.баллов:10
| Ответ: | A |
|---|---|
6. Объектно-ориентированное программирование
Разработать классы с наследованием, инкапсуляцией и полиморфизмом
Сложность:4
Макс.баллов:20
Ответ: _______________________
5. Базовые алгоритмы сортировки
Реализовать алгоритмы сортировки: пузырьковую, выбором и вставками
ВОПРОСЫ
- Алгоритмы сортировки
ОТВЕТЫ
- bubble_sort(), selection_sort(), insertion_sort()
- null
Сложность:3
Макс.баллов:15
| Ответ: | A |
|---|---|
4. Интегрирование функций
Вычислить определенные и неопределенные интегралы для заданных функций
Сложность:4
Макс.баллов:20
Ответ: _______________________
3. Вычисление производных
Найти производные заданных функций, используя правила дифференцирования
Сложность:3
Макс.баллов:15
Ответ: _______________________
1. Решение квадратных уравнений
Найти корни квадратного уравнения \(ax² + bx + c = 0\) для различных значений коэффициентов
ВОПРОСЫ
- Формула дискриминанта для решения квадратных уравнений
- Еще одна КРАСИВАЯ формула дискриминанта квадратного уравнения
ОТВЕТЫ
- $x = (-b ± \sqrt(b² - 4ac)) / 2a$
- \(x = (-b ± \sqrt{(b² - 4ac))} / 2a\)
- $\text{альтернатива}$
Сложность:2
Макс.баллов:10
| Ответ: | A | B |
|---|---|---|